04 - Multi-agent
Large-scale distributed policy learning for networked systems utlizing algebraic structures and game theory
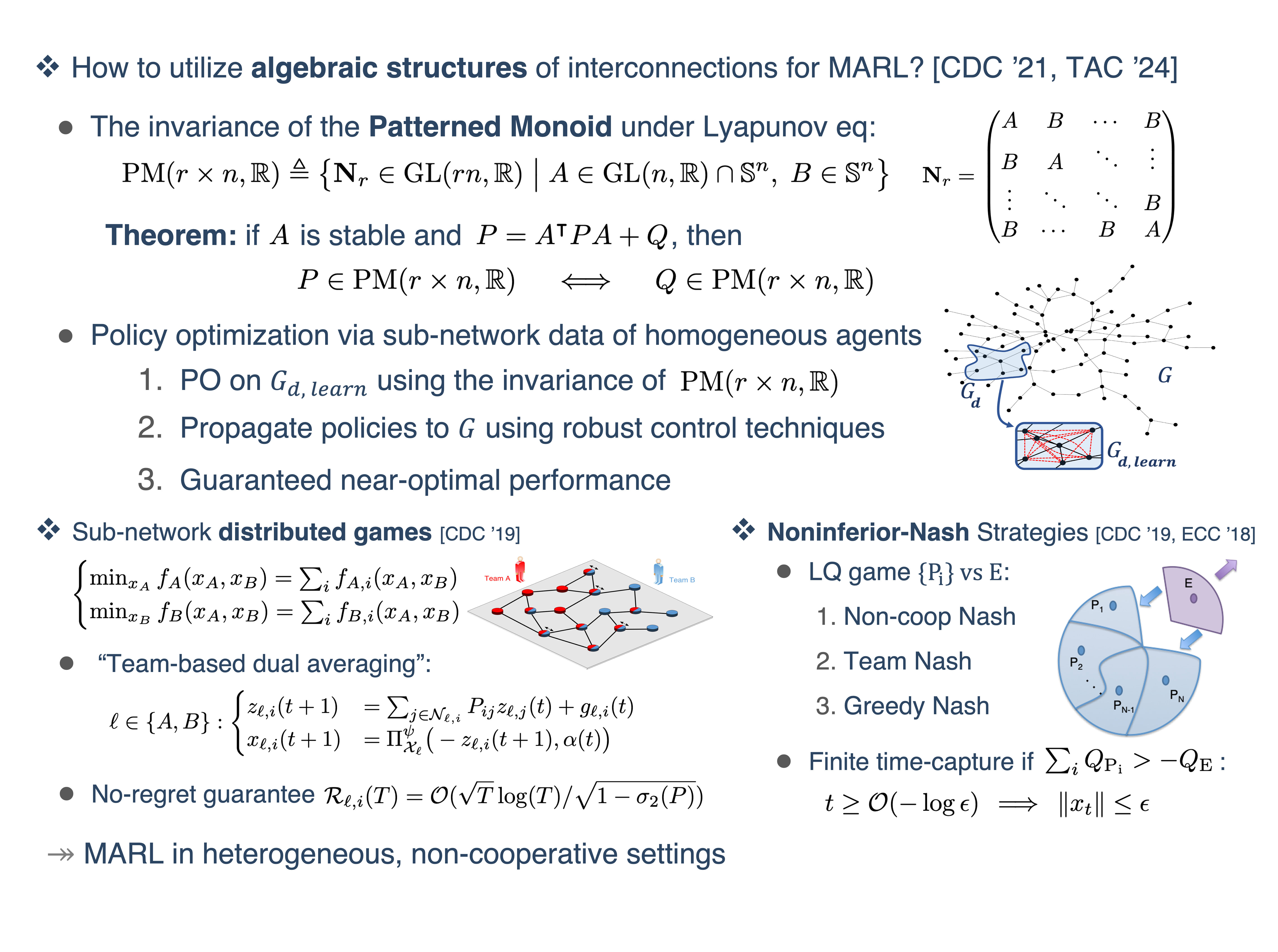
Even though these data-driven techniques are relatively well-studied for linear dynamical systems, they are not directly suitable for networked systems due to the associated computational complexity and information constraints involving the agents' interconnections. To resolve this issue, I characterized inherent symmetries and algebraic patterns, commonly arising in these large-scale complex systems, through the so-called Patterned Linear Semigroups (Talebi & others, 2021). The key idea, allowing us to extend data-driven methods to large-scale complex systems, is that this regular semigroup structure conforms with the construction of policy synthesis through the algebraic relations (e.g., Lyapunov equations). This approach can learn to (almost) optimally control a homogeneous network of dynamical agents only from a sub-network data. Furthermore, this procedure handles attaching/detaching agents on the fly without disrupting learning and control of the entire network (Talebi et al., 2024).
Additionally, complex dynamical systems often involve interacting agents making decisions for the collective benefit. However, disruptions or adversarial attacks can lead to conflicting decisions. I analyze these processes using cooperative and non-cooperative game theory, where agents adjust their strategies based on available information and environmental effects. My research extends game equilibrium to Noninferior Nash Strategies for agents with linear dynamics and quadratic criteria, providing theoretical guarantees for stability and overcoming attacks (Talebi et al., 2019; Talebi et al., 2019; Talebi & Simaan, 2017). I have also developed a simulation platform to efficiently predict outcomes based on system parameters (Talebi & Simaan, 2018).
In emerging resource-sharing enterprises like Uber or Lyft, companies operate over distributed sub-networks where assets are spread across a graph. In these 2-player games, agents lack complete information about their opponent's costs, motivating them to learn optimal strategies directly through their distributed interactions. I developed a no-regret algorithm for learning constrained policies across distributed sub-networks. Framing the problem as Variational Inequalities, each agent updates policies only based on local interactions and its private information, proving the convergent point to be Nash equilibria (Talebi et al., 2019).
Future Directions: I am building on this work to explore additional algebraic properties and network symmetries, aiming to create a unified framework for distributed reinforcement learning and data-driven control of heterogeneous agents. Also, I investigate non-cooperative settings beyond monotonicity, focusing on equilibria properties and last-iterate convergence that are critical in practical game scenarios beyond just regret minimization.
Key references:
-
Talebi, S., & others. (2021). Distributed Model-Free Policy Iteration for Networks of Homogeneous Systems. 2021 60th IEEE Conference on Decision and Control , 6970–6975.
-
Talebi, S., Alemzadeh, S., & Mesbahi, M. (2024). Data-Driven Structured Policy Iteration for Homogeneous Distributed Systems. IEEE Trans on Automatic Control (TAC), 69(9), 5979–5994.
-
Talebi, S., Simaan, M. A., & Qu, Z. (2019). Cooperative Design of Systems of Systems Against Attack on One Subsystem. 58th Conf on Decision and Control , 7313–7318.
-
Talebi, S., Simaan, M. A., & Qu, Z. (2019). Decision-making in complex dynamical systems of systems with one opposing subsystem. 18th European Control Conf, 2789–2795.
-
Talebi, S., & Simaan, M. A. (2017). Multi-pursuer pursuit-evasion games under parameters uncertainty: A Monte Carlo approach. 12th Sys. of Sys. Eng. Conf, 1–6.
-
Talebi, S., & Simaan, M. A. (2018). SIMPE: A Simulation Platform for Multi-Player Pursuit-Evasion Problems. 2018 IEEE 14th Int Conf on Control and Automation (ICCA).
-
Talebi, S., Alemzadeh, S., Ratliff, L. J., & Mesbahi, M. (2019). Distributed learning in network games: a dual averaging approach. 58th IEEE Conference on Decision and Control, 5544–5549.