01 - Geometry
Studying submanifolds of stabilizing policies for constrained optimal control problems using the Riemannian geometry inherent to the structure of these problems.
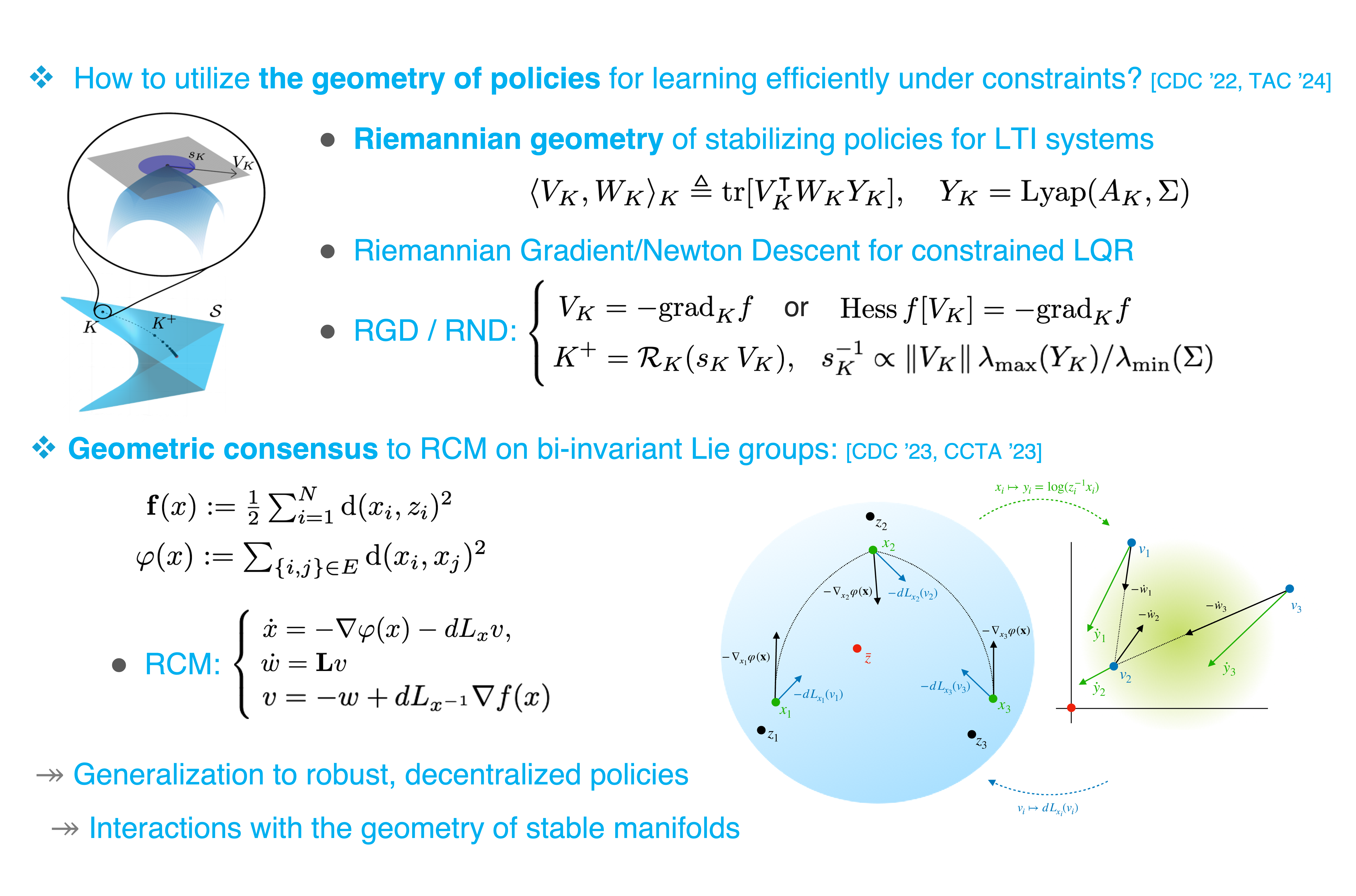
Iterative stability guarantees are essential in learning optimal policies in control systems, including policy optimization (PO) techniques. This challenge has been examined for problems with linear dynamics and quadratic cost structure (Fazel, et. al., ICML 2018), but in the absence of policy constraints. Furthermore, the non-Euclidean geometry of the stabilization problem in the context of policy optimization has often been overlooked. My research explores submanifolds of stabilizing policies for constrained optimal control problems using the Riemannian geometry inherent to the structure of these problems (Talebi & Mesbahi, 2022).
Through geometric techniques, this approach handles any linear constraint on the feedback policy under a unifying framework while providing an efficient numerical scheme that searches over the set of constrained stabilizing feedback policies. In addition to addressing foundational problems such as static output-feedback and structured linear quadratic regulator problems, it also facilitates handling intuitive but complicated constraints on the input energy, translated to nonlinear constraints on the policy (Talebi & Mesbahi, 2024).
Furthermore, extending these techniques to distributed geometric policy optimization requires developing fast backbone routines for consensus on manifolds, distinct from the standard consensus on Euclidean spaces. On that line, we have proposed a series of fast distributed algorithms for the Riemannian center of mass (Kraisler et al., 2023), and further considered the case of Lie groups using ideas from gradient tracking but extended to Riemannian manifolds (Kraisler et al., 2023).
Future Directions: To benchmark these advancements and outline future research, I led a recent survey in collaboration with leading researchers in the field, appearing in the Encyclopedia of Systems and Control Engineering (Talebi et al., 2024).
Key publications:
-
Talebi, S., & Mesbahi, M. (2022). Riemannian Constrained Policy Optimization via Geometric Stability Certificates. 2022 61th IEEE Conf on Decision and Control , 1472–1478.
-
Talebi, S., & Mesbahi, M. (2024). Policy optimization over submanifolds for linearly constrained feedback synthesis. IEEE Transactions on Automatic Control, 69(5), 3024–3039.
-
Kraisler, S., Talebi, S., & Mesbahi, M. (2023). Distributed consensus on manifolds using the Riemannian center of mass. 2023 IEEE Conf on Control Tech. and App., 130–135.
-
Kraisler, S., Talebi, S., & Mesbahi, M. (2023). Consensus on Lie groups for the Riemannian Center of Mass. 2023 62nd IEEE Conf on Decision and Control , 4461–4466.
-
Talebi, S., Zheng, Y., Kraisler, S., Li, N., & Mesbahi, M. (2024). Policy Optimization in Control: Geometry and Algorithmic Implications. In Encyclopedia of Systems and Control Theor (to appear). arXiv preprint arXiv:2406.04243. Elsevier.