Learning and Geometry

Constrained policy optimization on submanifolds of stabilizing controllers

In this project, we study optimization over the submanifolds of stabilizing controllers, equipped with a Riemannian metric arising from constrained Linear Quadratic Regulators (LQR) problems.

Let us illustrate this non-Euclidean geometry in the following example which arises from the structure of LQR problem:

(Left) An example of the non-convex feasible submanifold of stabilizing controllers. (Center) the orange subset on which the LQR cost has p.d. Euclidean Hessian. (Right) the blue subset on which the the LQR cost has p.d. Riemannian Hessian

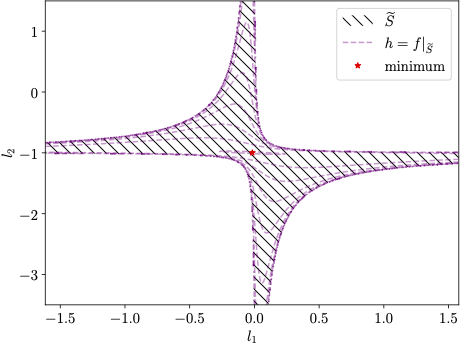
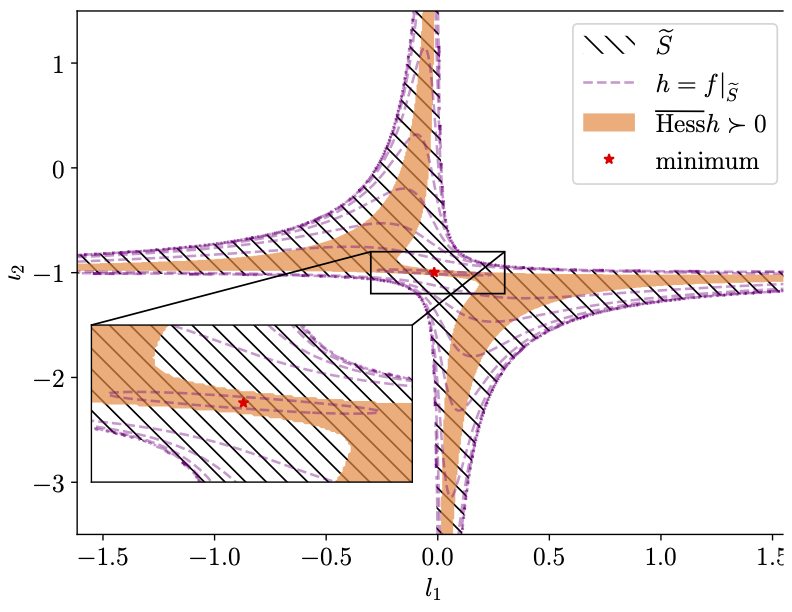
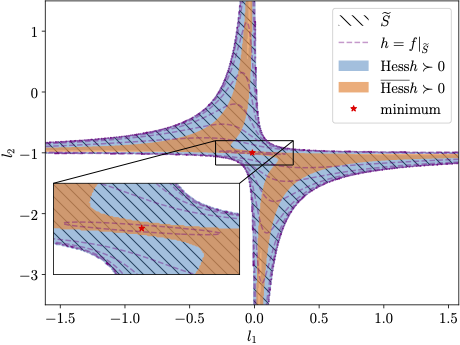
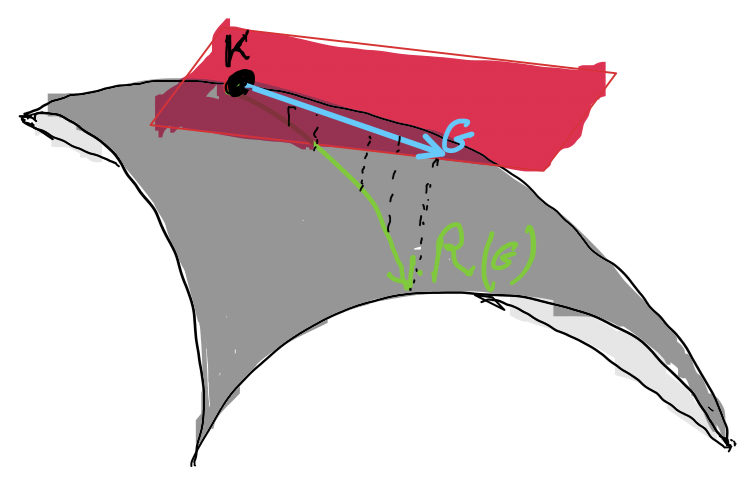
We provide a Newton-type algorithm that enjoys local convergence guarantees and exploits the inherent geometry of the problem. Instead of relying on the exponential mapping and in the absence of a global retraction, this algorithm revolves around the developed stability certificate as well as the linearity of the constraints. This idea can be illustrated in the following abstract form:

(Left) The abstract form of a retraction \( R(G) \) of a tangent vector \( G \) at the point \( K \). (Right) The stability certificate \( s_K \) at this point, and the corresponding local neighborhood of origin in \( T_K\mathcal{S} \) for which the retraction is possible.

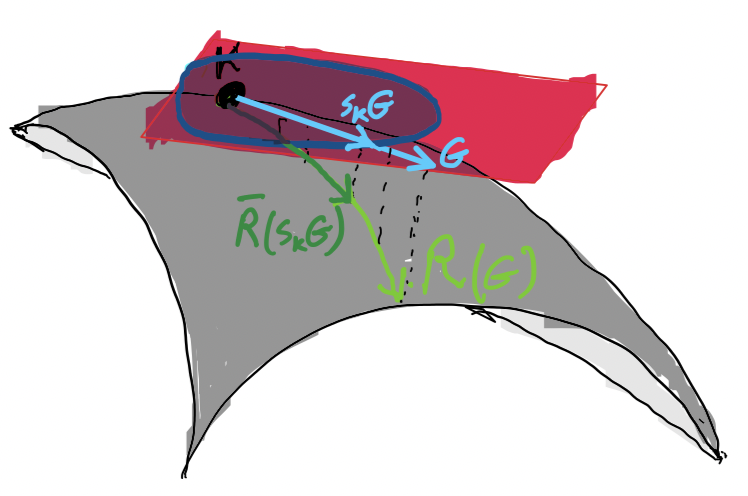
Let us now exemplify the proposed algorithm through numerical simulations in the context of Structured and Output-feedback LQR problems.

The trajectories of our algorithm using Riemaninan metric (blue) and Euclidean metric (orange) compared with the Projected Gradient (green) for the Strucutred LQR (left) and Output LQR (right) problems.
The algorithm at iteration \(t\) updates:
$$K^+ = K + \min\left\{s_{K}, 1\right\} \cdot G$$
where the Riemannian Newton direction \( G \) solves
$$\mathrm{Hess}\, h_{K}[G] = -\mathrm{grad}\, {h}_{K}.$$

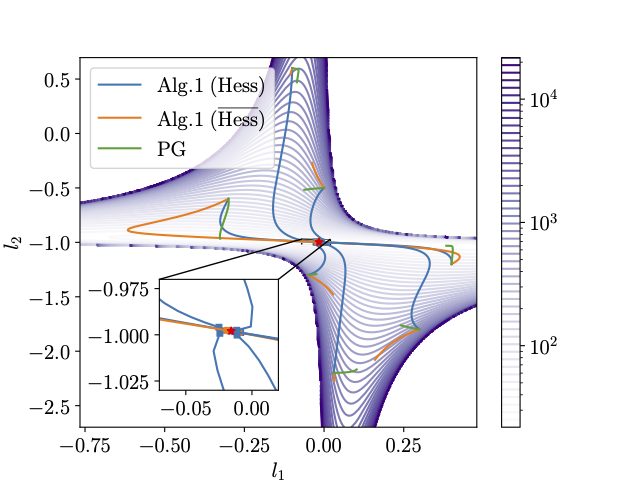
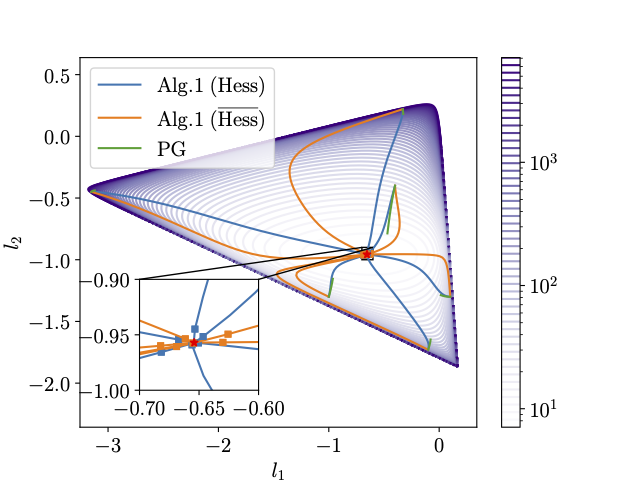
To better see the advantage of using the inherent non-Euclidean geometry, we can examine the performance this algorithm for 100 randomly samples parameters for these problems:

The min, max and median progress of normalized error and cost values for the (left) Structured LQR and (right) Output LQR problems.

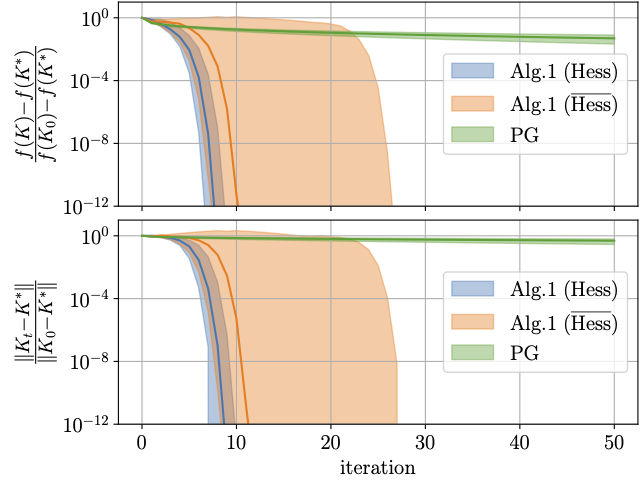
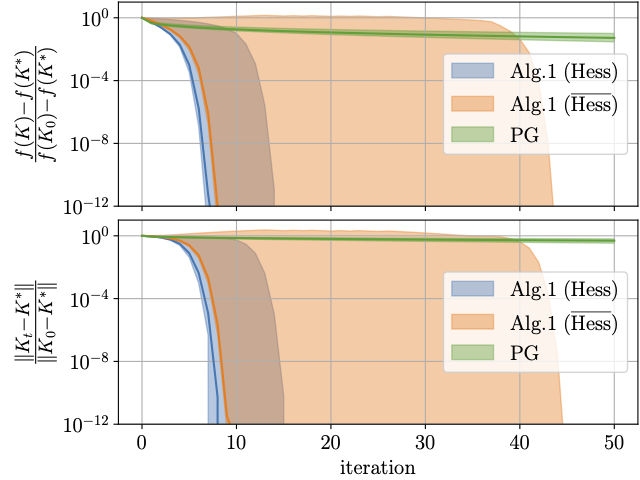
For more details and convergence guarantees, see this paper.